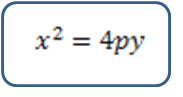Geometría Analítica
La geometría
analítica estudia las
figuras geométricas mediante técnicas básicas del análisis matemático
y del álgebra en un determinado sistema de coordenadas.
Los dos objetivos fundamentales de la
geometría analítica son:
•Dada una
curva en un sistema de coordenadas, obtener su ecuación.
•Dada la ecuación
indeterminada, polinomio, o función determinar en un sistema de
coordenadas la gráfica o curva algebraica de los puntos que
verifican dicha ecuación.
En
un sistema de coordenadas, los puntos del plano se representan por dos valores:abscisa (x) y ordenada (y), se escribe (x,y) . En la figura se han marcado algunos puntos.
Cónicas
•Se denomina sección
cónica (o
simplemente cónica) a
todas las curvas resultantes de las diferentes intersecciones entre
un cono y un plano. Se clasifican en cuatro
tipos: elipse, parábola, hipérbola y circunferencia.
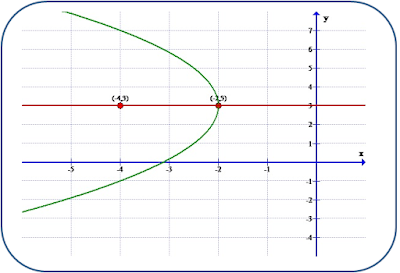
La Parábola
La Parábola es una sección cónica y se define como el lugar
geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco, y de una recta fija
llamada directriz.
1. El foco (F) es un punto siempre fijo.
2. El vértice (V) de la parábola es el punto de
intersección de la parábola con el eje de simetría. Es el punto medio del
segmento que une la directriz y el foco.
3. La directriz es una recta fija perpendicular al eje de simetría.
4. La distancia entre el
foco y la directriz de una parábola recibe el nombre de parámetro
de la parábola (2p).
5. La distancia entre el
vértice y el foco, llamada distancia focal, representado por p.
6. El
eje de la parábola
es la recta que contiene al foco y es perpendicular a la directriz.
7. El lado
recto, es el segmento de
recta comprendido por la parábola, que pasa por el foco y es paralelo a la
directriz y perpendicular al foco. Su longitud es siempre 4 veces la
distancia focal (4p).
 Elementos de la parábola:
Elementos de la parábola:
•Vértice: Punto V
•Foco: Punto F
•Lado recto: 4p
•Directriz: Recta L
•Eje: Recta que pasa
por el foco, el vértice y es perpendicular al lado recto y a la directriz
•P(x,y): un punto
cualquiera de la parábola
Posiciones de la Parábola
1.Vértice en el origen
1.1 Eje en el eje x
a) Se abre a la derecha
b) Se abre a la izquierda
1.1 1. Vértice en el origen
1.2 1.2 Eje en el eje y
a) Se abre hacia arriba
b) Se abre hacia abajo
2. Vértice fuera
del origen
2.1 Eje paralelo al eje x
a) Se abre a la derecha
b) Se abre a la izquierda
2.Vértice fuera del
origen
2.2 Eje paralelo al eje y
Fuente: https://es.wikipedia.org/wiki/Geometr%C3%ADa_anal%C3%ADtica